【番外編】AI（機械学習）やってみた。【第4回】ソムリAIの改良（正規化）

ソムリAI（ワインの評価を機械学習で当てる「ソムリエ+AI」）はもういいかなと思っていたのですが、機械学習の教科書的な本を読んでいるといくつか改良ポイントが見えてきたので、実際に適用してみようと思います。

まずはデータの正規化という手法を試してみました。結論から言うと、あまり効果はなかったのです。。

ソムリAIの振り返り

ワインの成分とランクのデータに対して、決定木・ロジスティック回帰・ニューラルネットワークの3通りのモデルを使って機械学習を行い、モデルの精度を検証してきました。それぞれのソムリAIの性能はこんな感じでした。

どのモデルも概ね60％程度の精度でした。

改良その1：正規化

正規化とは

まずは正規化という手法を試してみます。標準化とも呼ばれます。正規化を行うことで尺度の異なるデータを比べやすくするとともに、はずれ値の影響を小さくすることができます。正規化には各データを平均0・標準偏差1に成形する手法と、各データを0から1の範囲に成形する手法の2つがあります。

前者は標準偏差が出てくることからも分かるように、データが正規分布に従うことを前提にした正規化手法です。元のデータが釣鐘型の分布になっている場合に有効です。後者は単純にデータの範囲を0から1の範囲に狭める手法であり、元のデータが一様分布の場合（規則性が無くランダムなように見える場合）に有効です。

どちらの手法でもデータの範囲を一定のレンジに狭めており、そうすることで異なる尺度のデータを比べやすくしつつ、はずれ値の影響を下げるのです。

正規化してみる

元データの分布を確認

前回同様のワインのデータを使って正規化してみます。まずはワインのデータを読み込んで表示してみます。ついでに機械学習で使うワインの成分と、ワインの評価にデータを分割しておきます。

【オリジナルのワインデータ】
UCI（University of California, Irvine：カリフォルニア大学アーバイン校）
http://archive.ics.uci.edu/ml/machine-learning-databases/wine-quality/winequality-red.csv

#入力データセットを読み込み
import pandas as pd #データハンドリング用ライブラリ呼び出し
data = pd.read_csv('winequality-red.csv', encoding='SHIFT-JIS')

#機械学習で求める解である「評価」以外の項目をdata_Xに、「評価」をdata_Yに格納
data_X = data.copy()
del data_X['評価']
data_Y = data['評価']

data.head() #読み込んだデータの先頭5行を出力

次に、ワインの成分である「酒石酸濃度」から「アルコール度数」までのデータの分布を可視化してみます。成分が全部で11個あり、1個ずつ描画していると面倒なので、subplotという機能を使って2×2で4個いっぺんに描画します。

#素データの分布を描画　その1
import numpy as np
import matplotlib.pyplot as plt
get_ipython().run_line_magic('matplotlib', 'inline')

fig1 = plt.figure()

#酒石酸濃度
x1 = data_X['酒石酸濃度']
h1 = fig1.add_subplot(2,2,1)
h1.hist(x1, bins=100)
h1.set_title('酒石酸濃度')
h1.set_ylabel('件数')
#酢酸濃度
x2 = data_X['酢酸濃度']
h2 = fig1.add_subplot(2,2,2)
h2.hist(x2, bins=100)
h2.set_title('酢酸濃度')
h2.set_ylabel('件数')

#クエン酸濃度
x3 = data_X['クエン酸濃度']
h3 = fig1.add_subplot(2,2,3)
h3.hist(x3, bins=100)
h3.set_title('クエン酸濃度')
h3.set_ylabel('件数')

#残糖濃度
x4 = data_X['残糖濃度']
h4 = fig1.add_subplot(2,2,4)
h4.hist(x4, bins=100)
h4.set_title('残糖濃度')
h4.set_ylabel('件数')

#描画
plt.tight_layout() #タイトルのかぶりを防ぐおまじない
fig1.show()

当たり前ですが、データによって尺度がぜんぜん違いますね。また、幅は違えど「クエン酸濃度」以外は釣鐘型の正規分布っぽく見えます。

残りのデータについても同様に描画します（変数名を変えるだけなのでコードは省略します）。

概ね釣鐘型に見えます。ということで、平均0・標準偏差1にする正規化をしてみようと思います。

正規化

実際に計算式を書いて計算してみます。データの平均や標準偏差を求める関数が標準装備されているので、短いコードで記述できます。

#データの正規化（自分で平均・分散を算出するやり方）
data_X_norm = data_X.loc[:,data_X.columns].apply(lambda x : ((x - x.mean())*1/x.std()+0),axis=0)

#正規化した結果の確認（平均が0、標準偏差が1になっていればOK）
print('平均：')
print(round(data_X_norm.mean()))
print('標準偏差：')
print(round(data_X_norm.std()))

計算誤差の関係でマイナスの符号がついたりしていますが、平均0・標準偏差1になりました。

ちなみに、scikit-learnのpreprocessingという関数を使ってサクッと正規化することもできます。

#データの正規化　その2（scikit-learnの関数を使うやり方）
#こっちだとDataFrame型から配列に方が変わるので、注意
from sklearn import preprocessing
data_X_norm = preprocessing.scale(data_X)

#正規化した結果の確認（平均が0、分散が1になっていればOK）
print(round(data_X_norm.mean()), data_X_norm.std())

【参考にしたサイト】

【Python】数量データの正規化 ( 標準化 ) について - St_Hakky’s blog

[Python]pandasのデータフレームを標準化（偏差値化）する | On Your Mark . Tokyo

正規化したデータを描画

正規化したデータの分布を描画してみます。下段の正規化前のデータ分布と比較すると、分布の形は同じですが、尺度が変わっています。

正規化したデータ分布

正規化前のデータ分布

正規化したデータで機械学習

正規化したデータを使って機械学習をしてみます。まずはワインデータを機械学習のモデルを作る「訓練用」と、作ったモデルの汎化性能（未知のデータに対してどの程度有効かを測定すること）を測定するための「検証用」に分割します。前回同様、70%を訓練用・30%を検証用にします。

#正規化した入力データセットの70%を訓練データ・30%を検証データに分割
from sklearn.model_selection import train_test_split #機械学習用ライブラリ呼び出し
X_train, X_test, Y_train, Y_test = train_test_split(data_X_norm, data_Y,random_state=0, test_size=0.3)

決定木

はじめに断っておくと、決定木では正規化してもモデルの性能は変わりません。決定木は、与えられたデータの中で分類に有効なデータ（分類するにあたって優先度の高いデータ）の順位をつけて、上位のデータから順に分類していきます。そのため、各データの尺度が変わっても分布の形状が同じであれば分類する際の優先度が変わらないのです。

そのため、「正規化したデータでも性能が変わらないこと」を検証します。

#決定木の機械学習
from sklearn.tree import DecisionTreeClassifier #機械学習用ライブラリから決定木を呼び出し
treeModel = DecisionTreeClassifier(max_depth=4, random_state=0) #決定木モデルの定義
treeModel.fit(X_train, Y_train) #機械学習実行（訓練用データを使ったモデル生成）

from sklearn import metrics
print(metrics.accuracy_score(Y_train, treeModel.predict(X_train))) #訓練データの精度表示
print(metrics.accuracy_score(Y_test, treeModel.predict(X_test))) #検証用データの精度表示

訓練用で61.30％、検証用で59.17%なので正規化前と同じ精度となっています。

ロジスティック回帰

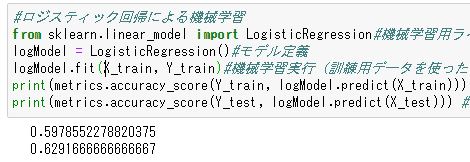
次にロジスティック回帰に正規化したデータを突っ込んでみます。

#ロジスティック回帰による機械学習
from sklearn.linear_model import LogisticRegression#機械学習用ライブラリからロジスティック回帰を呼び出し

logModel = LogisticRegression()#モデル定義
logModel.fit(X_train, Y_train)#機械学習実行（訓練用データを使ったモデル生成）

print(metrics.accuracy_score(Y_train, logModel.predict(X_train))) #訓練データの精度表示
print(metrics.accuracy_score(Y_test, logModel.predict(X_test))) #検証用データの精度表示

訓練用で59.79%・検証用で62.92%なので、訓練用の性能が微妙に上がったものの、検証用の性能はかわらずでした。。

ニューラルネットワーク

正規化前のベストなパラメータで機械学習

続いてニューラルネットワークに正規化したデータを突っ込みます。とりあえず、正規化前のソムリAIのニューラルネットワークにそのまま入れてみます。正規化前のソムリAIのベストなパラメータは、活性化関数がハイパボリックタンジェントという双曲線関数・ニューラルネットワークの階層が100･100･100･10の4階層でした。

#ニューラルネットワークによる機械学習
from sklearn.neural_network import MLPClassifier #機械学習用ライブラリからニューラルネットワークを呼び出し
mlpModel = MLPClassifier(activation='tanh', random_state=0, hidden_layer_sizes=(100,100,100,10)) #モデル定義
mlpModel.fit(X_train, Y_train) #機械学習実行
print(metrics.accuracy_score(Y_train, mlpModel.predict(X_train))) #訓練データの精度表示
print(metrics.accuracy_score(Y_test, mlpModel.predict(X_test))) #検証用データの精度表示

正規化したことで訓練データの精度が62.20%から94.46%に跳ね上がりました。ただ、検証データの精度は62.50%から61.04%に微減しています。訓練データの精度が高いのに検証データの精度が低いということは典型的な過学習を表しています。

グリッドサーチで最適なパラメータを探索（ざっくりと絞り込み）

過学習を起こしており、他にベストなパラメータがある可能性が高いのでグリッドサーチで探索してみます。ニューラルネットワークのパフォーマンスへの影響の大きい活性化関数（activation）・ソルバー（solver）・パーセプトロンの階層（hidden_layer_sizes）の3つで総当たりでベストなパラメーターを探索します。パーセプトロンの階層については1つの階層に10個・100個・200個、階層数を3階層・4階層用意して幅広に探索してみます。

#グリッドサーチで最適解を探す
from sklearn.model_selection import GridSearchCV

#シミュレーションするパラメータを定義

parameters = {'hidden_layer_sizes': [(10,10,10),(10,10,10,10),(100,100,10),(100,100,100),(100,100,100,10),
                                    (200,200,20),(200,200,200),(200,200,200,200)],
             'activation': ['logistic', 'identity', 'relu', 'tanh'],
             'solver': ['lbfgs', 'sgd', 'adam']}

#グリッドサーチの実行
mlpModel2 = GridSearchCV(MLPClassifier(random_state=0, max_iter=1000, early_stopping=True), parameters)
mlpModel2.fit(X_train, Y_train) #ベストな隠れ層を使った機械学習
mlpModel2.best_params_ #ベストな隠れ層の結果表示

待つこと20分強、活性化関数はrelu（Rectified linear unit）と呼ばれる区分線型関数（シグモイド関数のような滑らかな関数ではなく、カクカクしたようなもの）・ソルバーはlbfgs・階層は1階層200個を3階層がベストということでした。

得られたパラメータで機械学習してみます。

#ニューラルネットワークによる機械学習
from sklearn.neural_network import MLPClassifier #機械学習用ライブラリからニューラルネットワークを呼び出し
mlpModel = MLPClassifier(activation='relu', random_state=0, hidden_layer_sizes=(200,200,200), solver='lbfgs') #モデル定義
mlpModel.fit(X_train, Y_train) #機械学習実行
print(metrics.accuracy_score(Y_train, mlpModel.predict(X_train))) #訓練データの精度表示
print(metrics.accuracy_score(Y_test, mlpModel.predict(X_test))) #検証用データの精度表示

訓練データに対する精度は脅威の100%ですが、検証データに対する精度は62.5%で変わらず。過学習の傾向がより強くなる結果になりました。

グリッドサーチで最適なパラメータを探索（範囲を絞って絞り込み）

先ほどのグリッドサーチではパーセプトロンの数と階層数（hidden_layer_sizes）を幅広にざっくり決めたのですが、探索結果として(200,200,200）がよさげとのことだったので、ここをもう少し絞り込んでみようと思います。

具体的には先ほどのグリッドサーチの結果を踏まえて、活性化関数とソルバー、ネットワークの階層数を固定して、1階層あたりのパーセプトロンの数を変えてみようと思います。階層数は3階層で固定し、パーセプトロンの数を150・200・250・300などにして再度グリッドサーチをかけます。幅広に探索して得られた結果を元により最適なパラメータを求めるために絞り込んでいくイメージです。

#グリッドサーチで最適解を探す
from sklearn.model_selection import GridSearchCV

#シミュレーションするパラメータを定義
parameters = {'hidden_layer_sizes': [(150,150,150),(200,200,200),(250,250,250),(300,300,300),
                                     (500,500,500),(1000,1000,1000)],
                                     'activation': ['relu'],
                                    'solver': ['lbfgs']}

#グリッドサーチの実行
mlpModel2 = GridSearchCV(MLPClassifier(random_state=0, max_iter=1000, early_stopping=True), parameters)
mlpModel2.fit(X_train, Y_train) #ベストな隠れ層を使った機械学習
mlpModel2.best_params_ #ベストな隠れ層の結果表示